Douzi's Blog
0%

机器学习

发表于 更新于 分类于
本文字数： 12k 阅读时长 ≈ 11 分钟

1. 导学

  • 如何使用算法
  • 如何评价算法的好坏
  • 如何解决过拟合和欠拟合
  • 如何调节算法的参数
  • 如何验证算法的正确性

1.1 要求

1.2 如何使用算法

  • 如何评价算法的好坏
  • 如何解决过拟合和欠拟合
  • 如何调节算法的参数
  • 如何验证算法的正确性

2. 机器学习的数据

2.1 样本

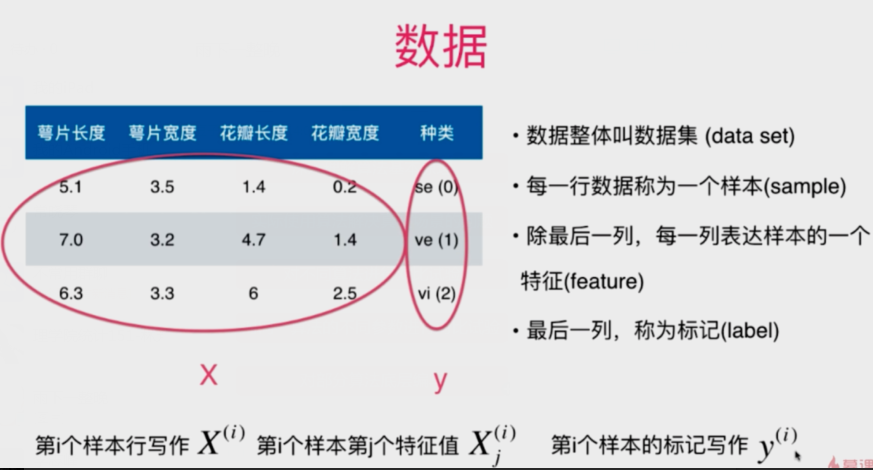
2.2 特征

2.3 特征空间

3. 机器学习分类

3.1 监督学习

给机器的训练数据拥有 “标记” 或者 “答案”

  • k近邻
  • 线性回归和多项式回归
  • 逻辑回归
  • SVM
  • 决策树和随机森林

3.2 非监督学习

给机器的训练数据没有任何“标记” 或者 “答案”

对没有“标记”的数据进行分类--聚类分析

意义：

  • 对数据进行降维处理
    • 特征提取： 信用卡的信用评级 和 人的胖瘦无关？
    • 特征压缩： PCA （不损失数据的情况下，将高维数据压缩成低维数据）
    • 降维处理的意义：方便可视化
  • 异常检测：

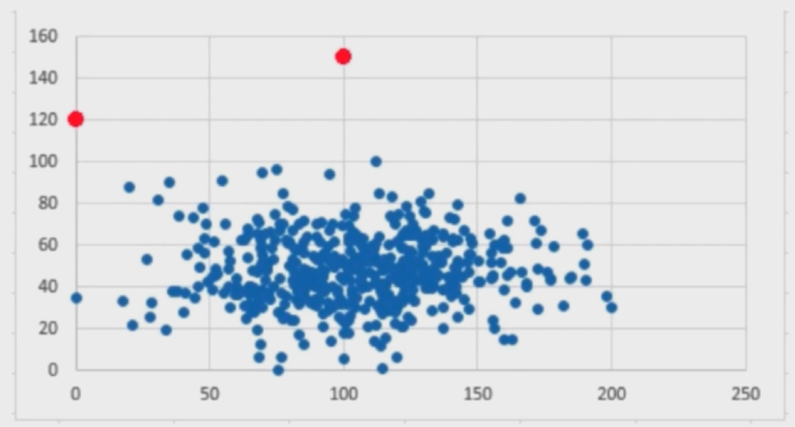
3.3 半监督学习

一部分数据有“标记” 或者 “答案“， 另一部分数据没有

更常见：各种原因产生的标记缺失

通常都先使用 无监督学习手段对数据做处理，之后使用 监督学习手段做模型的训练和预测

3.4 增强学习

  • 无人驾驶
  • 机器人

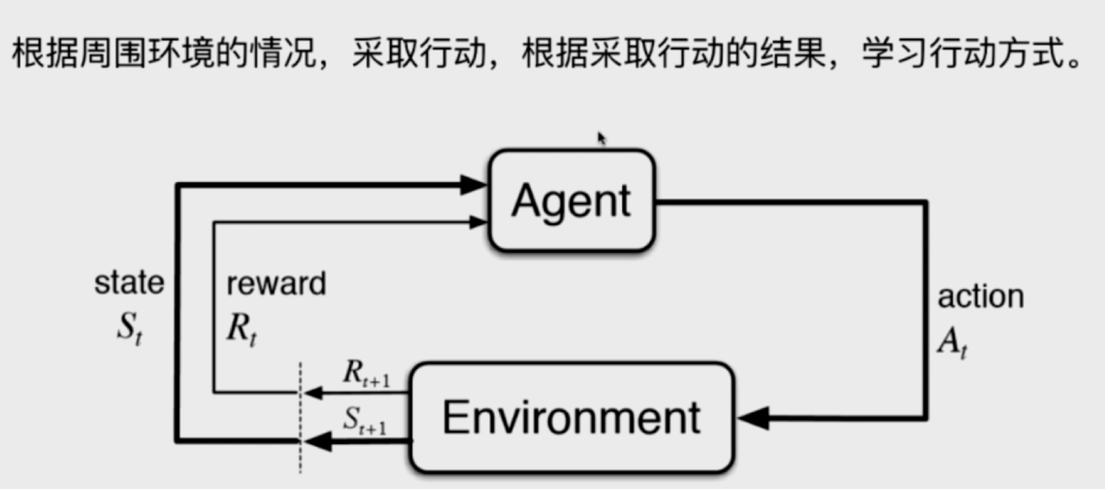
4. 机器学习的其他分类

4.1 在线学习和批量学习

  • 批量学习 Batch Learning（离线学习, 为主）

  • 优点： 简单

  • 问题：如何适应环境变化
    • 解决方案：定时重新批量学习

  • 缺点：每次重新批量学习，运算量巨大;

  • 在线学习 Online Learning

  • 优点：及时反映新的环境变化

  • 问题：新的数据带来不会的变化
    • 解决方案：需要加强对数据进行监控

  • 其他：也适用于数据量巨大，完全无法批量学习的环境

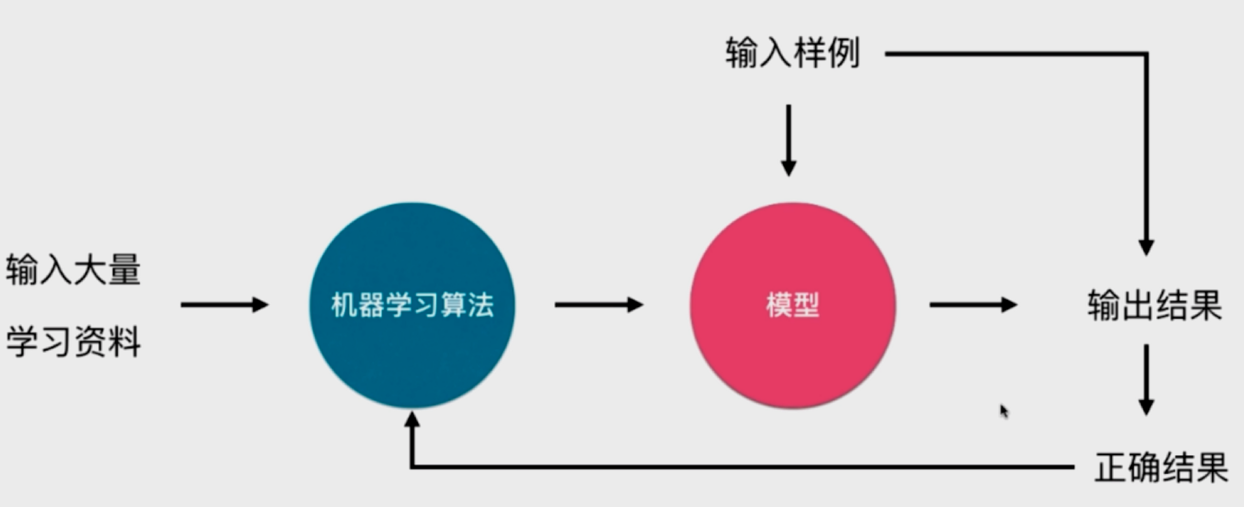
4.2 参数学习和非参数学习

  • 参数学习 Parametric Learning

一旦学到参数，就不再需要原有的数据集

  • 非参数学习 Nonparametric Learning
  • 不对模型进行过多假设
  • 非参数不等于没参数

5. 监督学习任务

5.1 分类任务

  • 二分类
  • 判断邮件是否为垃圾邮件
  • 判断发给客户信用卡是否有风险
  • 判断病患是良性肿瘤；恶性肿瘤
  • 判断股票涨跌
  • 多分类
  • 手写数字识别
  • 图像识别
  • 判断发给客户信用卡的风险评级
  • 2048游戏：转换为多分类，是否上移动，下移，左移等
  • 围棋
  • 无人车：根据环境信息，设置方向盘，油门、刹车
  • 多分类的任务可以转换成二分类任务
  • 多标签分类

一个图片分到多个类别

5.2 回归任务

  • 结果是一个连续的数字的值，而非一个类别
  • 房屋预测
  • 市场分析
  • 学生成绩
  • 股票价格
  • 一般情况下，回归任务可以简化成分类任务
  • 无人驾驶

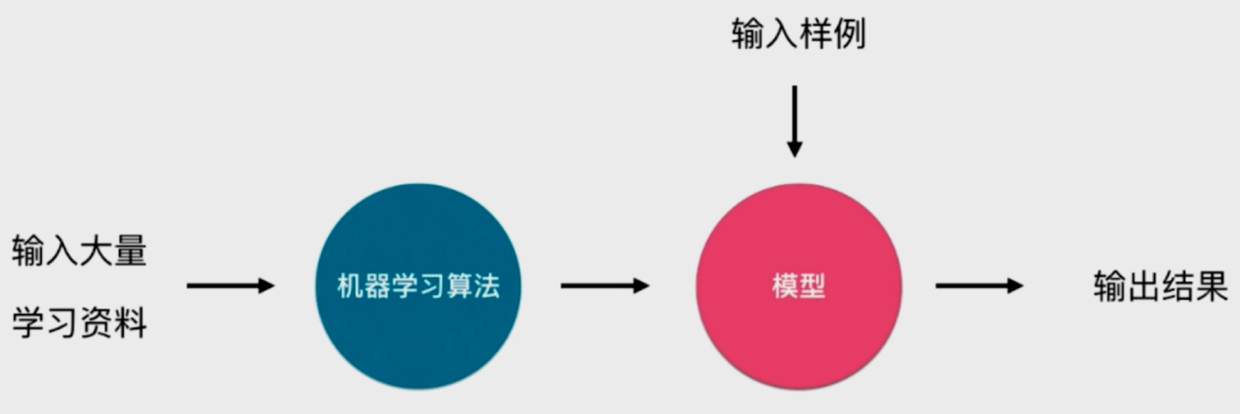
5.3 工作流程

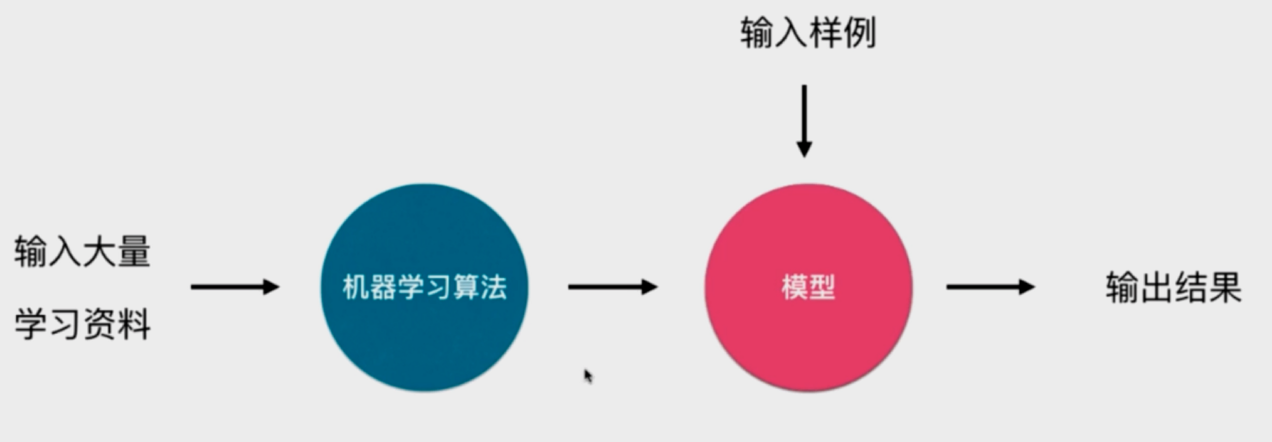
6. jupyter notebook

6.1 快捷键

1
2
3
4
5
run cell: ctrl + enter
change cell to md: m
change cell to code: c
delete cell: x
line number: L

6.2 魔法命令

  • %run：在 jupyter 中加载 .py文件代码
1
2
3
%run ./magic.py              # ./为文件路径

[out1]: hello('python')
1
2
3
4
import MagicTest.FirstML  # 导入magictest的模块
MagicTest.FirstML.predict(1)

[out2]: predict: ?
1
2
3
4
from MagicTest import FirstML
FirstML.predict(2)

[out3]: predict: ?
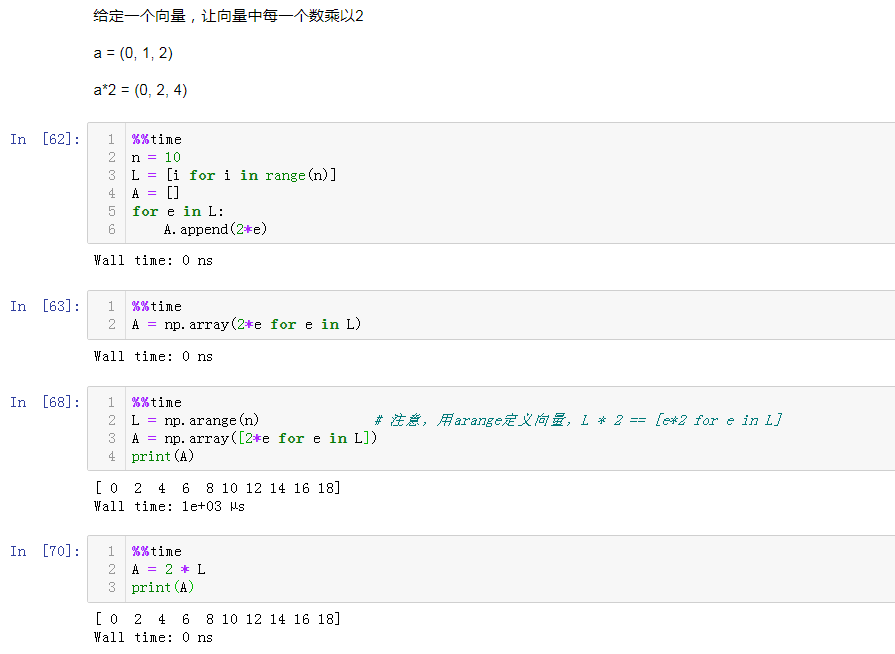
  • %timeit: 测试代码性能
1
2
3
%timeit L = [i**2 for i in range(1000)]

[out1]: 535 µs ± 11.4 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
1
2
3
%timeit L = [i**2 for i in range(10000000)]

[out1]: 5.89 s ± 923 ms per loop (mean ± std. dev. of 7 runs, 1 loop each)
1
2
3
4
5
6
%%timeit
L = []
for n in range(1000):
    L.append(n ** 2)
    
[out]: 603 µs ± 16.8 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)

%time: 代码计时(不用重复)

1
2
3
%time L = [i**2 for i in range(1000)]

[out1]: Wall time: 1e+03 µs
1
2
3
4
5
6
%%time
L = []
for i in range(1000):
    L.append(i**2)
    
[out2]: Wall time: 2 ms
  • 其他魔法命令
1
2
3
4
5
6
7
8
9
10
%lsmagic

[out1]: 
Available line magics:
%alias  %alias_magic  %autoawait  %autocall  %automagic  %autosave  %bookmark  %cd  %clear  %cls  %colors  %conda  %config  %connect_info  %copy  %ddir  %debug  %dhist  %dirs  %doctest_mode  %echo  %ed  %edit  %env  %gui  %hist  %history  %killbgscripts  %ldir  %less  %load  %load_ext  %loadpy  %logoff  %logon  %logstart  %logstate  %logstop  %ls  %lsmagic  %macro  %magic  %matplotlib  %mkdir  %more  %notebook  %page  %pastebin  %pdb  %pdef  %pdoc  %pfile  %pinfo  %pinfo2  %pip  %popd  %pprint  %precision  %prun  %psearch  %psource  %pushd  %pwd  %pycat  %pylab  %qtconsole  %quickref  %recall  %rehashx  %reload_ext  %ren  %rep  %rerun  %reset  %reset_selective  %rmdir  %run  %save  %sc  %set_env  %store  %sx  %system  %tb  %time  %timeit  %unalias  %unload_ext  %who  %who_ls  %whos  %xdel  %xmode

Available cell magics:
%%!  %%HTML  %%SVG  %%bash  %%capture  %%cmd  %%debug  %%file  %%html  %%javascript  %%js  %%latex  %%markdown  %%perl  %%prun  %%pypy  %%python  %%python2  %%python3  %%ruby  %%script  %%sh  %%svg  %%sx  %%system  %%time  %%timeit  %%writefile

Automagic is ON, % prefix IS NOT needed for line magics.
1
%run?   # 查看文档

7. numpy和matplotlib

7.1 Numpy

7.11 Numpy.array

  • 使用一：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np

L = [i for i in range(10)]
print(L)
L[5] = 'Machine Learning'
print(L)

import array
arr = array.array('i', [i for i in range(10)])  # 只能定义一种类型
print(arr)
arr[5] = 100
print(arr)

nparr = np.array([i for i in range(10)])      # 只能定义一种类型
print(nparr)
print(nparr.dtype)

nparr = np.array([1, 2, 3.0])   # float
print(nparr.dtype)

[out1]: 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[0, 1, 2, 3, 4, 'Machine Learning', 6, 7, 8, 9]
array('i', [0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
array('i', [0, 1, 2, 3, 4, 100, 6, 7, 8, 9])
[0 1 2 3 4 5 6 7 8 9]
int32
float64
  • 使用二：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# 全为0，默认浮点型
print('=================np.zero===================')
print(np.zeros(10))
print(np.zeros(10).dtype)                     
print(np.zeros(10, dtype=int)) 
print(np.zeros(shape=(3, 5), dtype=int))

print('=================np.ones===================')
# 全为1，默认浮点型
print(np.ones(10))          # 向量
print(np.ones( (3, 5) ))    # 矩阵

print('=================np.full=================')
# 指定值
print(np.full(shape=(3, 5), fill_value=666))   # 为指定类型
print(np.full(shape=(3, 5), fill_value=666.0))

print('=================np.full=================')
# arange
print(np.arange(0, 1, 0.2))   # 可以有浮点数

# linspace
print('=================np.linspace===================')
print(np.linspace(0, 20, 10))   # [0,20]区间，生成10个等差数列

# random
print('=================np.random===================')
np.random.seed(100)
print(np.random.randint(0, 1, 10))   # [0, 1), 不包含1
print(np.random.randint(4, 8, size=(3, 5)))
print(np.random.randint(4, 8, size=10))

# 生成10个0-1之间均匀的浮点数
print(np.random.random(10))

# 正态分布
print(np.random.normal())
print(np.random.normal(10, 100))  # [10, 100)
print(np.random.normal(0, 1, (3, 5)))



[out1]:
=================np.zero===================
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
float64
[0 0 0 0 0 0 0 0 0 0]
[[0 0 0 0 0]
 [0 0 0 0 0]
 [0 0 0 0 0]]
=================np.ones===================
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[[1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]
 [1. 1. 1. 1. 1.]]
=================np.full=================
[[666 666 666 666 666]
 [666 666 666 666 666]
 [666 666 666 666 666]]
[[666. 666. 666. 666. 666.]
 [666. 666. 666. 666. 666.]
 [666. 666. 666. 666. 666.]]
=================np.full=================
[0.  0.2 0.4 0.6 0.8]
=================np.linspace===================
[ 0.          2.22222222  4.44444444  6.66666667  8.88888889 11.11111111
 13.33333333 15.55555556 17.77777778 20.        ]
=================np.random===================
[0 0 0 0 0 0 0 0 0 0]
[[4 4 7 7 7]
 [7 4 6 6 4]
 [6 5 6 6 6]]
[6 5 4 4 7 4 7 4 6 4]
[0.56229626 0.00581719 0.30742321 0.95018431 0.12665424 0.07898787
 0.31135313 0.63238359 0.69935892 0.64196495]
-0.23028508500632336
58.09241158682933
[[-1.26691058  0.27100509  2.14076322  0.47536904  0.24652489]
 [-1.08417396 -2.3815826  -0.4363488  -2.07241186 -1.29543984]
 [-0.46402358 -0.05702664  0.27592974  1.49451522  0.56682064]]
  • 查询相应文档
1
2
np.random?
help(np.random.normal)

7.12 numpy基本操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
import numpy as np

x = np.arange(10)
print('x: ', x)

# 转换 维度
X = np.arange(15).reshape(3, 5)
print('X:', X)

# 基本属性
print('x维度:', x.ndim)    # 查看维度属性
print('X维度:', X.ndim)
print('X.shape: ', X.shape)
print('X.size: ', X.size)

# numpy.array的数据访问
print('X:', X)
print('X[0][0]: (不推荐)', X[0][0])
print('X[2, 2]: (推荐) ', X[2, 2])
print('X[:2, :3]: (前2行前3列)', X[:2, :3])
print('X[:2][:3]: (预料不符)', X[:2][:3])
print('X[:2, ::2]: ', X[:2, ::2])
print('X[: , 0]: (取一列) ', X[:, 0])

subX = X[:2, :3]         # 浅拷贝
print("subX:", subX)
print("X: ", X)

X[0, 0] = 999
print("subX:", subX)
print("X: ", X)

# 深拷贝
subX = X[:2, :3].copy()
X[0, 0] = 888
print("subX:", subX)
print("X: ", X)

# Reshape
print('x.shape: ', x.shape)
A = x.reshape((2, 5))
print('x.reshape(2, 5): ', A)

# 只想要十行
tenlines = x.reshape(10, -1)    # 每行元素自动计算
print("转换为10行: ", tenlines)


[out]:
x:  [0 1 2 3 4 5 6 7 8 9]
X: [[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]
x维度: 1
X维度: 2
X.shape:  (3, 5)
X.size:  15
X: [[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]
X[0][0]: (不推荐) 0
X[2, 2]: (推荐)  12
X[:2, :3]: (前2行前3列) [[0 1 2]
 [5 6 7]]
X[:2][:3]: (预料不符) [[0 1 2 3 4]
 [5 6 7 8 9]]
X[:2, ::2]:  [[0 2 4]
 [5 7 9]]
X[: , 0]: (取一列)  [ 0  5 10]
subX: [[0 1 2]
 [5 6 7]]
X:  [[ 0  1  2  3  4]
 [ 5  6  7  8  9]
 [10 11 12 13 14]]
subX: [[999   1   2]
 [  5   6   7]]
X:  [[999   1   2   3   4]
 [  5   6   7   8   9]
 [ 10  11  12  13  14]]
subX: [[999   1   2]
 [  5   6   7]]
X:  [[888   1   2   3   4]
 [  5   6   7   8   9]
 [ 10  11  12  13  14]]
x.shape:  (10,)
x.reshape(2, 5):  [[0 1 2 3 4] [5 6 7 8 9]]
[[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]]

7.13 合并操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
x = np.array([1, 2, 3])
y = np.array([3, 2, 1])
print('x: ', x)
print('y: ', y)

# 合并操作
print("合并x, y: ", np.concatenate([x, y]))

z = np.array([666, 666, 666])
print('合并x, y, z: ', np.concatenate([x, y, z]))

A = np.array([[1,2,3], [4, 5, 6]])
print('合并两个A: ', np.concatenate([A, A]))

# 沿着不同维度来合并操作
# axis = 0: 按行来拼接
# axis = 1 按列来拼接
print('axis=0: ', np.concatenate([A, A], axis=0))
print('axos=1: ', np.concatenate([A, A], axis=1))

# 将向量和矩阵合并(按行)，不能使用concatenate
print('A和x合并: ', np.concatenate([A, x.reshape(1, -1)]))
      
print('使用vstack来拼接A和x: (按行)', np.vstack([A, x]))

B = np.full((2, 2), 100)
print('使用hstack来拼接A和B: (按列)', np.hstack([A, B]))

[out1]:
x:  [1 2 3]
y:  [3 2 1]
合并x, y:  [1 2 3 3 2 1]
合并x, y, z:  [  1   2   3   3   2   1 666 666 666]
合并两个A:  [[1 2 3]
 [4 5 6]
 [1 2 3]
 [4 5 6]]
axis=0:  [[1 2 3]
 [4 5 6]
 [1 2 3]
 [4 5 6]]
axos=1:  [[1 2 3 1 2 3]
 [4 5 6 4 5 6]]
A和x合并:  [[1 2 3]
 [4 5 6]
 [1 2 3]]
使用vstack来拼接A和x: (按行) [[1 2 3]
 [4 5 6]
 [1 2 3]]
使用hstack来拼接A和B: (按列) [[  1   2   3 100 100]
 [  4   5   6 100 100]]

7.14 分割操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
x = np.arange(10)
print('x: \n', x)

x1, x2, x3 = np.split(x, [3, 7])
print('x1: \n', x1)
print('x2: \n', x2)
print('x3: \n', x3)

print('='*20)
A = np.arange(16).reshape((4, 4))
print('A: \n', A)

A1, A2 = np.split(A, [2])           # np.vsplit(A, [2]): 从第二行开始分割 
print('A1: \n', A1)
print('A2; \n', A2)
 
B1, B2 = np.split(A, [2], axis=1)   # np.hsplit(A, [2]): 从第二列开始分割
print('B1: \n', B1)
print('B2: \n', B2)

print('='*20)
data = np.arange(16).reshape((4, 4))
x, y =  np.hsplit(data, [-1])     # 分离特征 和 标签值
print('x: \n', x)
print('y: \n', y)

[out1]:
x: 
 [0 1 2 3 4 5 6 7 8 9]
x1: 
 [0 1 2]
x2: 
 [3 4 5 6]
x3: 
 [7 8 9]
====================
A: 
 [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
A1: 
 [[0 1 2 3]
 [4 5 6 7]]
A2; 
 [[ 8  9 10 11]
 [12 13 14 15]]
B1: 
 [[ 0  1]
 [ 4  5]
 [ 8  9]
 [12 13]]
B2: 
 [[ 2  3]
 [ 6  7]
 [10 11]
 [14 15]]
====================
x: 
 [[ 0  1  2]
 [ 4  5  6]
 [ 8  9 10]
 [12 13 14]]
y: 
 [[ 3]
 [ 7]
 [11]
 [15]]

7.15 矩阵运算

  • 矩阵对应元素间运算：
    • A*2, A+2, np.exp(A)等都是对A中所有元素进行操作
    • A+B, A*B, A/B: 都是矩阵元素之间对应运算

  • 矩阵乘法:
    • A.dot(B)
  • 矩阵转置:
    • A.T
  • 矩阵的逆: \(A*A^{-1}=E\)
    • np.linalg.inv(A) (方阵)
    • 伪逆矩阵： np.linalg.pinv(x) (非方阵使用)

7.16 聚合操作

1
2
3
4
import numpy as np
data = np.random.rand(1000000)
%timeit = sum(data)
%timeit = np.sum(data)  # 更快
  • np.sum(A, axis=0) : 每一列的和
  • np.sum(A, axis=1) : 每一行的和
  • np.mean(X) : 均值
  • np.median(X) ： 中位数
  • np.percentile(X, q=50) : 求 50% 的数
  • np.var(X) : 方差
  • np.std(X) : 标准差

7.17 索引

1
2
3
np.min(x)
np.argmin(x)    # 返回 min的值的 索引值
np.argmax(x)    # 最大值索引

7.18 排序

  • np.sort(A, axis=1) ：默认为1，按行排序
    • axis=0 : 按列排序

  • np.argsort(x) ： 按照索引排序

  • np.partition(x, 3) : 3前面的数字都比他小，后面的都比他大

7.19 FancyIndexing

  • X[row, col]
    • row, col 为索引组成的向量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np 

x = np.arange(16)
print(x)

ind = [3, 5, 8]
print(x[ind])

X = x.reshape(4, -1)
print(X)

row = np.array([0, 1, 2, 3])
col = np.array([0, 1, 2, 3])
print("对角线元素: ", X[row, col])

[out1]:
[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
[3 5 8]
[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]
[ 0  5 10 15]
  • 重要: 使用bool值
    • a = [True, False, False, True]
    • X[a] : 这种用法很常用
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
print(x < 3)
print(x == 3)
print(x*2 == 25 - 4*x)

# 例子: 样本中有多少小于3岁的人
np.sum(x <= 3)
np.count_nonzero(x <= 3)

# 是否有为0的元素, 有任意一个数为 0 则返回True
np.any(x == 0)   
np.any(x < 0)   # 有一个 小于0 则返回 True
np.all(x > 0)   # 所有元素都 > 0 则返回 True

print(x)
np.sum(~(x==0))

print(X[X[:, 3] % 3 == 0, :])

7.2 matplotlib

10. 评价分类结果

10.1 混淆矩阵Confusion Matrix

10.2 精准率和召回率

精准率：预测有100个人有癌症，在这些预测中，有多少是准确的。 \(precision = \frac{TP}{TP + FP}\)

  • 需要的是精确度

召回率：实际上100人有癌症，我们的预测算法能从中正确的挑出多少。 \(recall = \frac{TP}{P} = \frac{TP}{TP + FN}\)

  • 需要的是预测的范围，预测的多不多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np
from sklearn import datasets

# 导入数据
digits = datasets.load_digits()        # 手写数字识别
X = digits.data
y = digits.target.copy()     # 深拷贝
# print(X)
# print(y)

y[digits.target==9] = 1      # 等于9的，  为1
y[digits.target!=9] = 0      # 不等于9的，为0

# 切割数据
from sklearn.model_selection import train_test_split
# 切分数据集为 训练集 和 测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

# 逻辑回归
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
print(log_reg.score(X_test, y_test))      # 这是准确度 

# 注意，此数据为 偏斜较大的数据，因此，需要考察其他指标
# 逻辑回归的预测值
y_log_predict = log_reg.predict(X_test)

# 对于混淆矩阵
# TN
def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 0))    # 预测为0，预测正确，y_true为 0

# TN 值
print(TN(y_test, y_log_predict))

# FP
def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 1))    # 预测为9，预测错误，y_true为 0

print(FP(y_test, y_log_predict))


def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 0))   # 预测成0，预测错误，y_true为 1

print(FN(y_test, y_log_predict))


def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 1))   # 预测成 9，预测正确，y_true为 1

print(TP(y_test, y_log_predict))


def confusion_matrix(y_true, y_predict):
    return np.array([
                     [TP(y_true, y_predict), FN(y_true, y_predict)],
                     [FP(y_true, y_predict), TN(y_true, y_predict)]
                    ])

confusion_matrix(y_test, y_log_predict)

# precision
def precision_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fp = FP(y_true, y_predict)
    try:
        return tp / (tp + fp)
    except:
        return 0.0
    
print("精准率: ", precision_score(y_test, y_log_predict))


# recall
def recall_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)
    try:
        return tp / (tp + fn)
    except:
        return 0.0
    
print("召回率:", recall_score(y_test, y_log_predict))
1
2
3
4
5
6
7
8
9
0.9755555555555555
403
2
9
36
[[ 36   9]
 [  2 403]]
精准率:  0.9473684210526315
召回率: 0.8